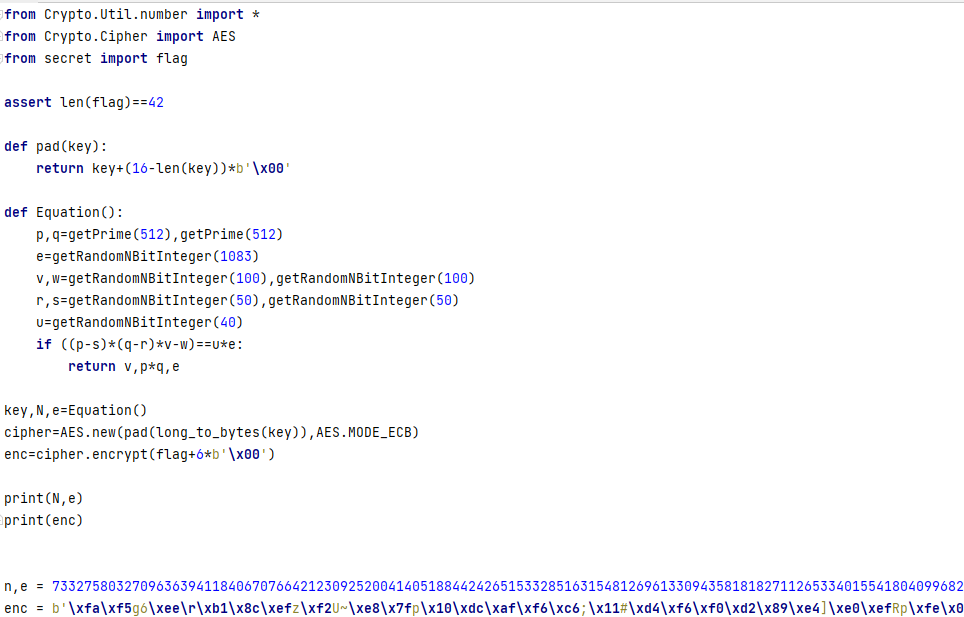
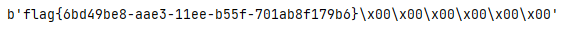在前天的科技节中遇到了一道winner的题目,一开始杯题目给误导了,以为是要列方程进行求解,赛后进行咨询发现使用winner直接可以求出关键的key,从而进行解密
在题目中可以得知e是和n差不多大的数,一开始想过要使用winner,但看到后面的方程直接使用z3列了方程,虽然到最后也没跑出来
对公式进行分解可以得到 k * n-a * p-b * q+s = u*e
连分数分解的意义:
分子(numerator):连分数逼近中的分子是 RSA 私钥 d 的候选值。
分母(denumerator):连分数逼近中的分母是对应的 k,满足
e * d - k * phi(n) = 1
其中phi(n) = (p-1) *(q-1)
对连分数进行展开即可得到题目中的公式,由此可知key为连分数的分母k,而题目中限定了key的位数,因此进行筛选即可得到key,从而进行求解得到flag
代码如下
``
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class ContinuedFraction(): def __init__(self, numerator, denumerator): self.numberlist = [] # number in continued fraction self.fractionlist = [] # the near fraction list self.GenerateNumberList(numerator, denumerator) self.GenerateFractionList() def GenerateNumberList(self, numerator, denumerator): while numerator != 1: quotient = numerator // denumerator remainder = numerator % denumerator self.numberlist.append(quotient) numerator = denumerator denumerator = remainder def GenerateFractionList(self): self.fractionlist.append([self.numberlist[0], 1]) for i in range(1, len(self.numberlist)): numerator = self.numberlist[i] denumerator = 1 for j in range(i): temp = numerator numerator = denumerator + numerator * self.numberlist[i - j - 1] denumerator = temp self.fractionlist.append([numerator, denumerator]) a = ContinuedFraction(e, n) # for k, d in a.fractionlist: # if k.bit_length() == 100: # print(k) key = 802055116687584857500947940756 def pad(key): return key+(16-len(key))*b'/x00' cipher=AES.new(pad(long_to_bytes(key)),AES.MODE_ECB) flag=cipher.decrypt(enc) print(flag)
运行即可得到flag